Anders Hesselboms teknikblogg

Lorenz vattenhjul

2021-07-03

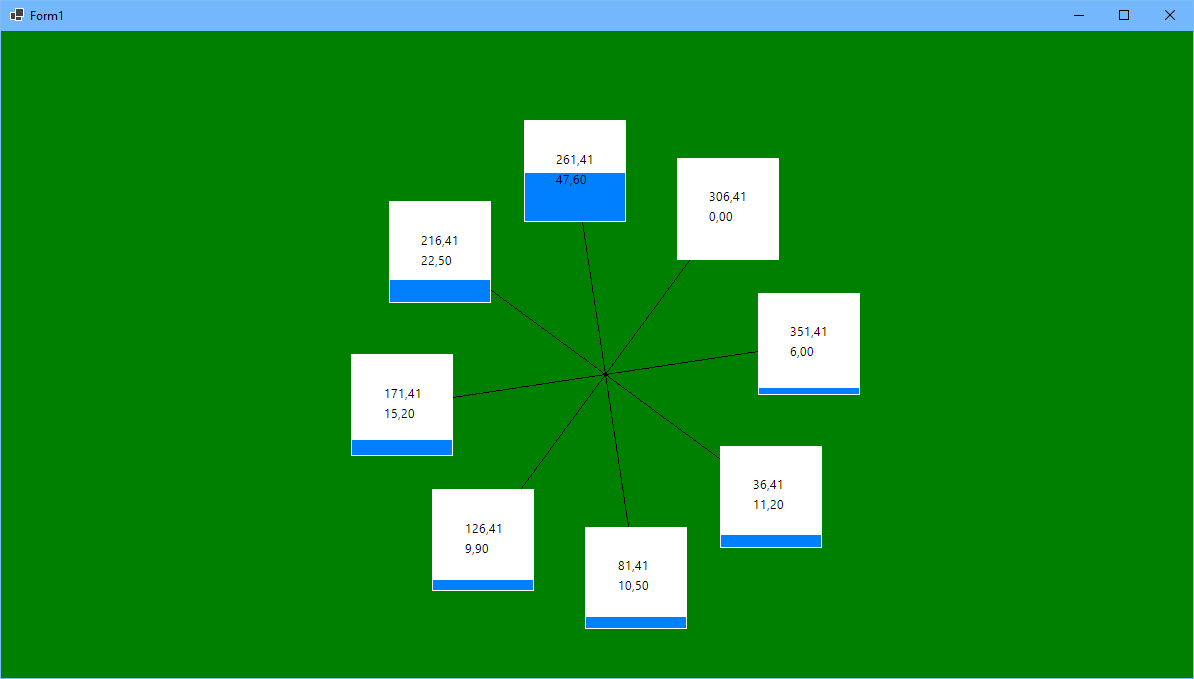
Lorenz-attraktionen är en fraktal vars formel beskriver en rotationshastighet (illustrerat med en radie) och en rotationsriktning. Så här ser den ut, implementerad i Commodore BASIC 7.0:

10 GRAPHIC 1,1
20 X=5
30 Y=5
40 Z=5
50 T=0
60 S=1/200
70 D=10
80 R=28
90 B=8/3
100 T=T+0.1
110 DX=D*(Y-X)
120 X1=X+DX*S
130 DY=(R*X-Y)-X*Z
140 Y1=Y+DY*S
150 DZ=X*Y-B*Z
160 Z1=Z+DZ*S
170 X=X1
180 Y=Y1
190 Z=Z1
200 DRAW 1,150+4*X,20+3*Z
210 IF T<1000 GOTO 100

Det går att bygga ett riktigt vattenhjul som ger samma figur som algoritmen ovan. Tänk dig ett hjul med ett antal hinkar (t.ex. åtta stycken). Den hink som är högst upp fylls på med vatten, och att du ger hjulet en knuff så att det roterar åt höger. På det viset kommer nästa hink strax börja fyllas med vatten, vilket ger en vikt på hjulets högra sida, så att rotationshastigheten ökar. Men alla hinkar har ett hål i botten, så när de inte ökar i vikt för att de fylls med vatten, så minskar de i vikt. När hinkarna når den uppåtgående vänstersidan av hjulet, väger de mycket mindre, vilket bidrar till att rotationshastigheten ökar. Men om rotationshastigheten ökar, så minskar samtidigt mängden vatten som fylls på i hinken högst upp, eftersom hinken befinner sig kortare tid vid positionen för påfyllning. Det innebär att den tyngsta sidan inte alltid kommer vara högersidan, eftersom den höga rotationshastigheten och den låga påfyllningen får vikten att förflytta sig. Ibland roterar alltså hjulet åt höger, ibland åt vänster. Ibland roterar hjulet fort, ibland långsamt.

Centralt i implementationen av denna simulering är en funktion som kan omvandla en vinkel på hjulet till en rotationskraft. Högst upp eller längst ner på hjulet, kommer vikten inte att påverka hjulets vilja att rotera alls. Längst till höger eller längst till vänster är kraften som störst. Vid 0 grader och vid 180 grader ska kraften vara 0, vid 90 och 270 grader är kraften maximal. Följande funktion är central för implementationen. Den beskriver hur starkt grepp gravitationen har över hinken – ingen alls högst upp eller längst ner, väldigt mycket längst till höger eller vänster.

Math.Cos(angle / (180.0 / Math.PI));

Implementationen av hjulet har 8 entiteter (“hinkar”) utplacerade med jämna mellanrum. 8 genom 350 ger 45 graders mellanrum. Den lilla knuffen åt höger får ha värdet 0,2 så att rotationen kommer igång.

var angle = 0;
for (var i = 0; i < 8; i++)
{
    Wheel.Buckets.Add(new Bucket(Wheel, angle));
    angle += 45;
}
Wheel.Speed = 0.2;

För hjulets beteende gäller följande: Hastigheten (som är positiv för höger och negativ för vänster) adderas till vinkeln. Därefter kontrollerar vi att vinkeln ligger mellan 0 och 360. Därefter berättar vi för varje hjul vilken vinkel de sitter på, givet hjulets vinkel, och ber samtidigt hjulet att agera (nedan). Sedan räknar vi ut hur hinkkonfigurationen påverkar hastigheten, och kontrollerar samtidigt att maxhastigheten åt höger eller vänster inte överstiger hjulets tänkta maxhastighet.

public void Tick()
{
    Angle += Speed;
    if (Angle < 0.0)
        Angle += 360.0;
    else if (Angle > 360.0)
        Angle -= 360.0;

    var bucketAngle = Angle;

    for (var i = 0; i < 8; i++)
    {
        if (bucketAngle < 0.0)
            bucketAngle += 360.0;
        else if (bucketAngle > 360.0)
            bucketAngle -= 360.0;
            
        Buckets[i].Tick(bucketAngle);
        bucketAngle += 45.0;
    }
    Speed += SpeedInfluence();
    const double maxSpeed = 7.0;
    if (Speed > maxSpeed)
        Speed = maxSpeed;
    else if (Speed < -maxSpeed)
        Speed = -maxSpeed;
}

public double SpeedInfluence() =>
    Buckets.Sum(x => x.SpeedInfluence());

För varje hinks beteende gäller följande: Om hinken är högst upp, öka vattenmängden, annars minska vattenmängden en aning. Varje hjul måste kunna uppge gravitationens grepp om hinken.

public void Tick(double newAngle)
{
    Angle = newAngle;
        
    if (Angle >= 255.0 && Angle <= 285.0)
        Full += 2.0;

    Full -= 0.12;
        
    if (Full < 0.0)
        Full = 0.0;
    else if (Full > 100.0)
        Full = 100.0;
}

public double SpeedInfluence() =>
    Math.Cos(Angle / (180.0 / Math.PI)) * (Full * 0.03);

Endast vattnet har vikt, hinkarna väger ingenting. Eftersom hjulet är balanserat och alla tomma hinkar väger lika mycket, kan vikten lika gärna vara 0.

Resultatet blir ett hjul som ibland snurrar fort, ibland långsamt, ibland åt höger och ibland åt vänster.

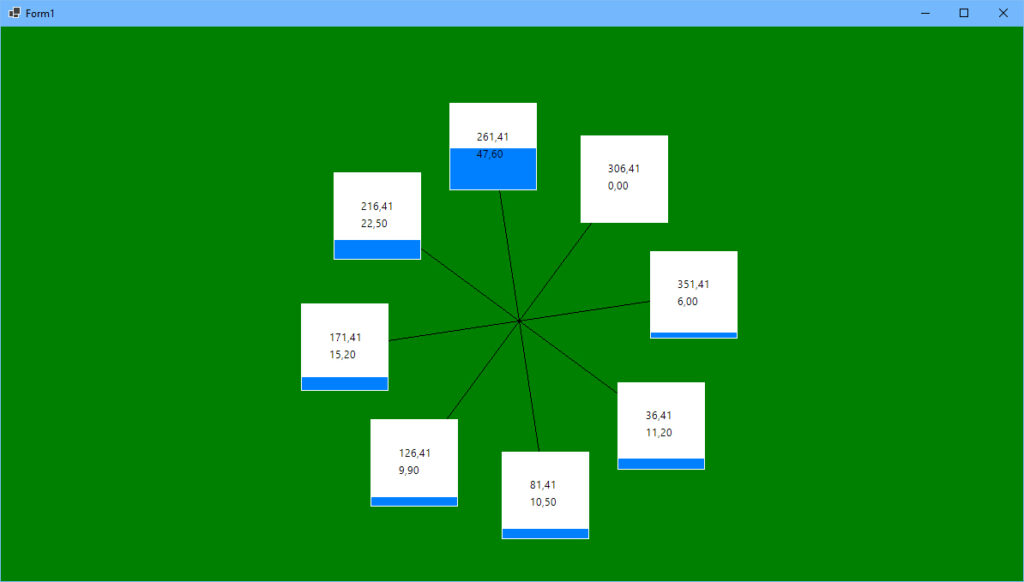
Koden körs i ett Windows Forms-fönster med DoubleBuffering aktiverat. Här är hela källkoden:

using System;
using System.Collections.Generic;
using System.Drawing;
using System.Linq;
using System.Windows.Forms;

public partial class Form1 : Form
{
    private Wheel Wheel { get; }

    public Form1()
    {
        InitializeComponent();
        Wheel = new Wheel();
        InitializeWheel();
    }

    private void InitializeWheel()
    {
        var angle = 0;
        for (var i = 0; i < 8; i++)
        {
            Wheel.Buckets.Add(new Bucket(angle));
            angle += 45;
        }
        Wheel.Speed = 0.2;
    }

    private void Form1_Paint(object sender, PaintEventArgs e)
    {
        var g = e.Graphics;
        g.Clear(Color.Green);

        var centerX = (Bounds.Width / 2);
        var centerY = (Bounds.Height / 2);
            
        var availableSize = Bounds.Width > Bounds.Height
            ? Bounds.Height
            : Bounds.Width;

        var radius = availableSize * 0.3;

        var renderer = new Renderer(centerX, centerY, (float)radius);
        renderer.Draw(g, Wheel, Font);
    }

    private void timer1_Tick(object sender, EventArgs e)
    {
        Wheel.Tick();
        Invalidate();
    }
}

public class Wheel
{
    public List<Bucket> Buckets { get; set; }
    public double Speed { get; set; }
    public double Angle { get; set; }

    public Wheel()
    {
        Buckets = new List<Bucket>();
        Angle = 0.0;
    }

    public void Tick()
    {
        Angle += Speed;
        if (Angle < 0.0)
            Angle += 360.0;
        else if (Angle > 360.0)
            Angle -= 360.0;

        var bucketAngle = Angle;

        for (var i = 0; i < 8; i++)
        {
            if (bucketAngle < 0.0)
                bucketAngle += 360.0;
            else if (bucketAngle > 360.0)
                bucketAngle -= 360.0;
            
            Buckets[i].Tick(bucketAngle);
            bucketAngle += 45.0;
        }
        Speed += SpeedInfluence();
        const double maxSpeed = 7.0;
        if (Speed > maxSpeed)
            Speed = maxSpeed;
        else if (Speed < -maxSpeed)
            Speed = -maxSpeed;
    }

    public double SpeedInfluence() =>
        Buckets.Sum(x => x.SpeedInfluence());
}

public class Bucket
{
    public double Weight { get; set; }
    public double Angle { get; set; }
    public double Full { get; set; }

    public Bucket(double angle)
    {
        Weight = 0.0;
        Angle = angle;
        Full = 0.0;
    }

    public void Tick(double newAngle)
    {
        Angle = newAngle;
        
        if (Angle >= 255.0 && Angle <= 285.0)
            Full += 2.0;

        Full -= 0.12;
        
        if (Full < 0.0)
            Full = 0.0;
        else if (Full > 100.0)
            Full = 100.0;
    }

    public double SpeedInfluence() =>
        Math.Cos(Angle / (180.0 / Math.PI)) * (Full * 0.03);

    public void Draw(Graphics g, PointF location, Font font)
    {
        using var bucketBrush = new SolidBrush(Color.FromArgb(255, 255, 255));
        using var waterBrush = new SolidBrush(Color.FromArgb(0, 128, 255));
        var bucketRectangle = new RectangleF(location.X - 51, location.Y - 51, 102, 102);
        g.FillRectangle(bucketBrush, bucketRectangle);
        if (Full > 0.0)
        {
            var waterRectangle = new RectangleF(location.X - 50, (float)(location.Y - 50 + (100.0 - Full)), 100, (float)Full);
            g.FillRectangle(waterBrush, waterRectangle);
        }
        g.DrawString(Angle.ToString("0.00"), font, Brushes.Black, (float)(location.X - 20), (float)(location.Y - 20));
        g.DrawString(Full.ToString("0.00"), font, Brushes.Black, (float)(location.X - 20), (float)(location.Y));
    }
}

public class Renderer
{
    private readonly PointF _center;
    private readonly float _radius;

    public Renderer(float centerX, float centerY, float radius)
    {
        _center = new PointF(centerX, centerY);
        _radius = radius;
    }

    public void Draw(Graphics g, Wheel wheel, Font font)
    {
        foreach (var bucket in wheel.Buckets)
        {
            var bucketLocation = new PointF(
                (float)(_center.X + Math.Cos(bucket.Angle / (180.0 / Math.PI)) * _radius),
                (float)(_center.Y + Math.Sin(bucket.Angle / (180.0 / Math.PI)) * _radius)
            );
            g.DrawLine(Pens.Black, _center, bucketLocation);
            bucket.Draw(g, bucketLocation, font);
        }
    }
}

Det går garanterat att justera acceleration, gravitation, inflödeshastighet, utflödeshastighet och maximal hastighet för andra (bättre?) resultat.

Categories: C#, General